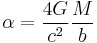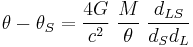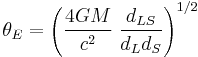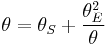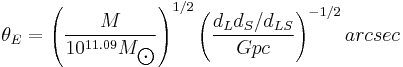Einstein radius

The Einstein radius is the radius of an Einstein ring, and is a characteristic angle for gravitational lensing in general, as typical distances between images in gravitational lensing are of the order of the Einstein radius.

Derivation

In the following derivation of the Einstein radius, we will assume that all of mass $M$ of the lensing galaxy $L$ is concentrated in the center of the galaxy.

For a point mass the deflection can be calculated and is one of the classical tests of general relativity. For small angles $\alpha$ the total deflection by a point mass $M$ is given (see Schwarzschild metric) by

$\alpha = \frac{4G}{c^2}\frac{M}{b}$

where

$b$ is the impact parameter (the distance of nearest approach of the lightbeam to the center of mass)

$G$ is the gravitational constant,

$c$ is the speed of light.

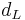By noting that, for small angles and with the angle expressed in radians, the point of nearest approach b at an angle $\theta$ for the lens $L$ on a distance $d_L$ is given by 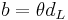$b =\theta d_L$ , we can re-express the bending angle $\alpha$ as

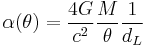$\alpha(\theta) = \frac{4G}{c^2}\frac{M}{\theta}\frac{1}{d_L}$ (eq. 1)

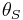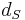If we set $\theta_S$ as the angle at which one would see the source without the lens (which is generally not observable), and $\theta$ as the observed angle of the image of the source with respect to the lens, then one can see from the geometry of lensing (counting distances in the source plane) that the vertical distance spanned by the angle $\theta$ at a distance $d_S$ is the same as the sum of the two vertical distances 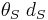$\theta_S \;d_{S}$ plus $\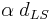alpha \;d_{LS}$ . This gives the lens equation,

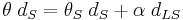$\theta \; d_S = \theta_S\; d_S %2B \alpha \; d_{LS}$ ,

which can be rearranged to give

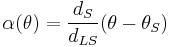$\alpha(\theta) = \frac{d_S}{d_{LS}} (\theta - \theta_S)$ (eq. 2)

By setting (eq. 1) equal to (eq. 2), and rearranging, we get

$\theta-\theta_S = \frac{4G}{c^2} \; \frac{M}{\theta} \; \frac{d_{LS}}{d_S d_L}$

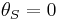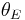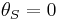For a source right behind the lens, $\theta_S=0$ , and the lens equation for a point mass gives a characteristic value for $\theta$ that is called the Einstein radius, denoted $\theta_E$ . Putting $\theta_S = 0$ and solving for $\theta$ gives

$\theta_E = \left(\frac{4GM}{c^2}\;\frac{d_{LS}}{d_L d_S}\right)^{1/2}$

The Einstein radius for a point mass provides a convenient linear scale to make dimensionless lensing variables. In terms of the Einstein radius, the lens equation for a point mass becomes

$\theta = \theta_S %2B \frac{\theta^2_E}{\theta}$

Substituting for the constants gives

$\theta_E = \left(\frac{M}{10^{11.09} M_{\bigodot}}\right)^{1/2} \left(\frac{d_L d_S/ d_{LS}}{Gpc}\right)^{-1/2} arcsec$

In the latter form, the mass is expressed in solar masses 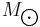$M_{\bigodot}$ and the distances in Gigaparsec (Gpc). The Einstein radius most prominent for a lens typically halfway between the source and the observer.

For a dense cluster with mass 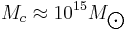$M_c \approx 10^{15} M_{\bigodot}$ at a distance of 1 Gigaparsec (1 Gpc) this radius could be as large as 100 arcsec (called macrolensing). For a Gravitational microlensing event (with masses of order 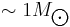$\sim 1 M_{\bigodot}$ ) search for at galactic distances (say $d\sim 3 kpc$ ), the typical Einstein radius would be of order milli-arcseconds. Consequently separate images in microlensing events are impossible to observe with current techniques.

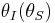The argument above can be extended for lenses which have a distributed mass, rather than a point mass, by using a different expression for the bend angle $\alpha$ . The positions $\theta_I(\theta_S)$ of the images can then be calculated. For small deflections this mapping is one-to-one and consists of distortions of the observed positions which are invertible. This is called weak lensing. For large deflections one can have multiple images and a non-invertible mapping: this is called strong lensing. Note that in order for a distributed mass to result in an Einstein ring, it must be axially symmetric.

References

Chwolson, O (1924). "Über eine mögliche Form fiktiver Doppelsterne". Astronomische Nachrichten 221 (20): 329–330. Bibcode 1924AN....221..329C. doi:10.1002/asna.19242212003. (The first paper to propose rings)
Einstein, Albert (1936). "Lens-like Action of a Star by the Deviation of Light in the Gravitational Field". Science 84 (2188): 506–507. Bibcode 1936Sci....84..506E. doi:10.1126/science.84.2188.506. JSTOR 1663250. PMID 17769014. (The famous Einstein Ring paper)
Renn, Jurgen; Tilman Sauer and John Stachel (1997). "The Origin of Gravitational Lensing: A Postscript to Einstein's 1936 Science paper". Science 275 (5297): 184–186. Bibcode 1997Sci...275..184R. doi:10.1126/science.275.5297.184. PMID 8985006.

Einstein radius

Derivation

References

See also